SWAG Publication

Abstract

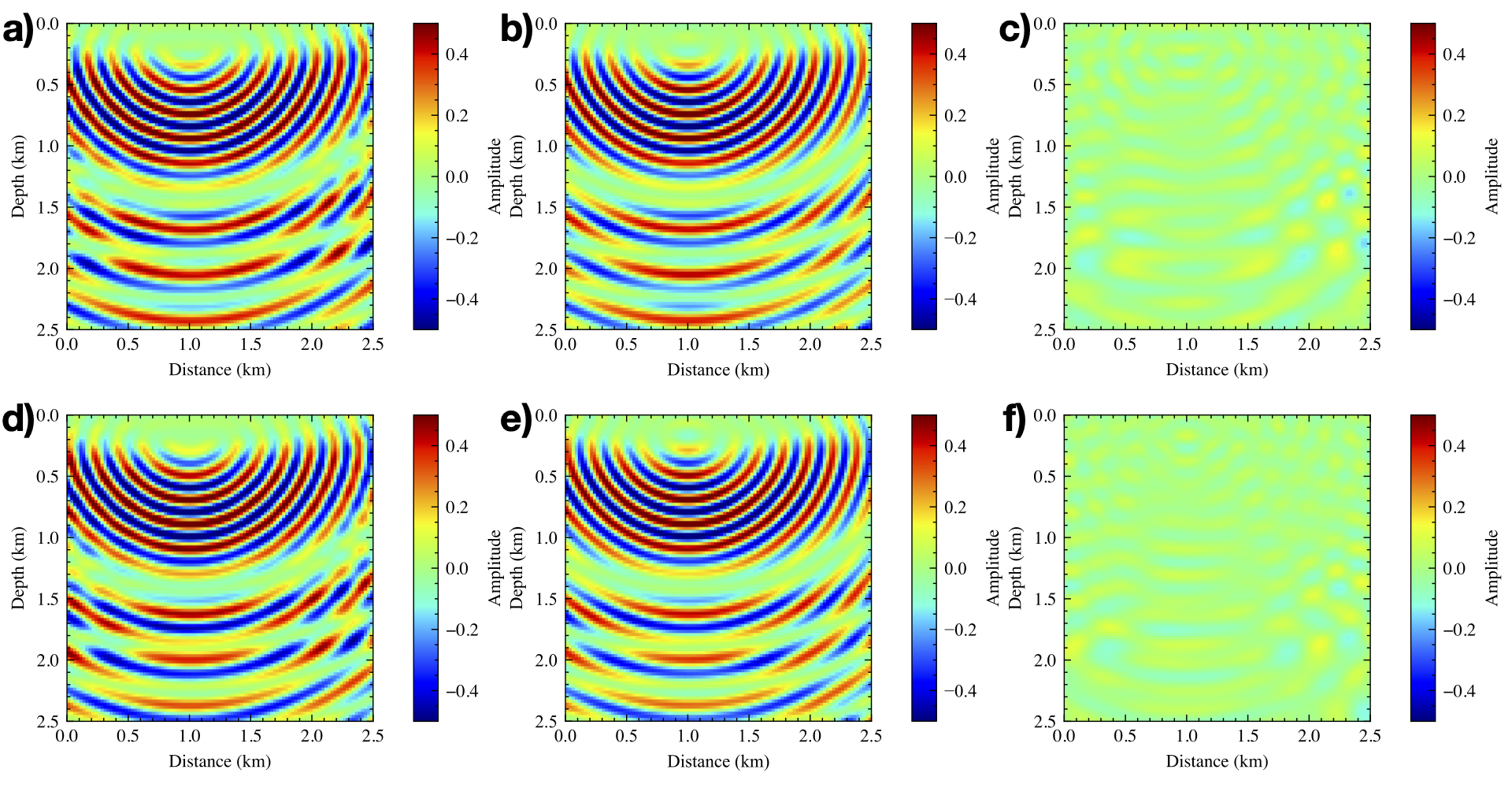
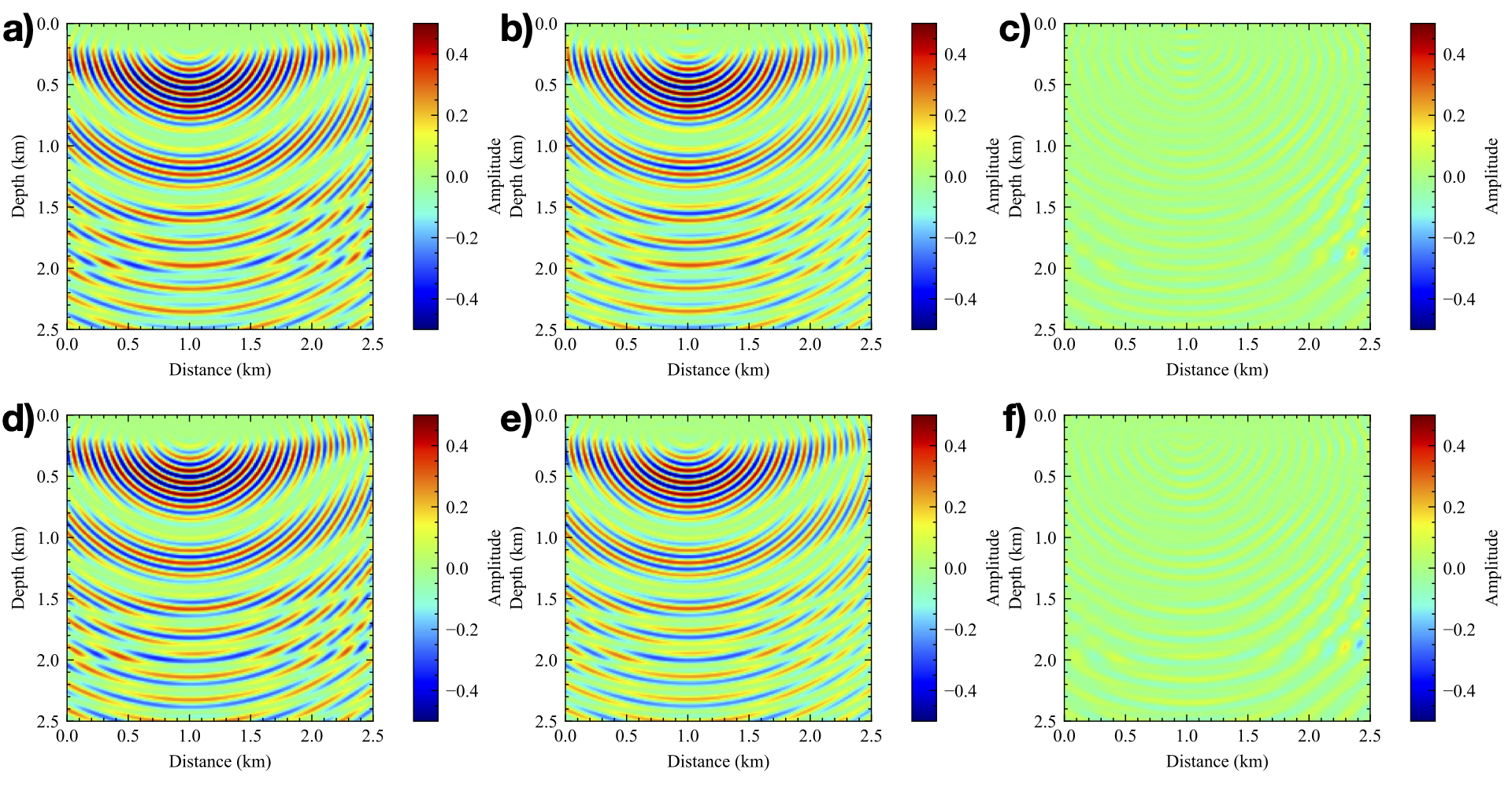
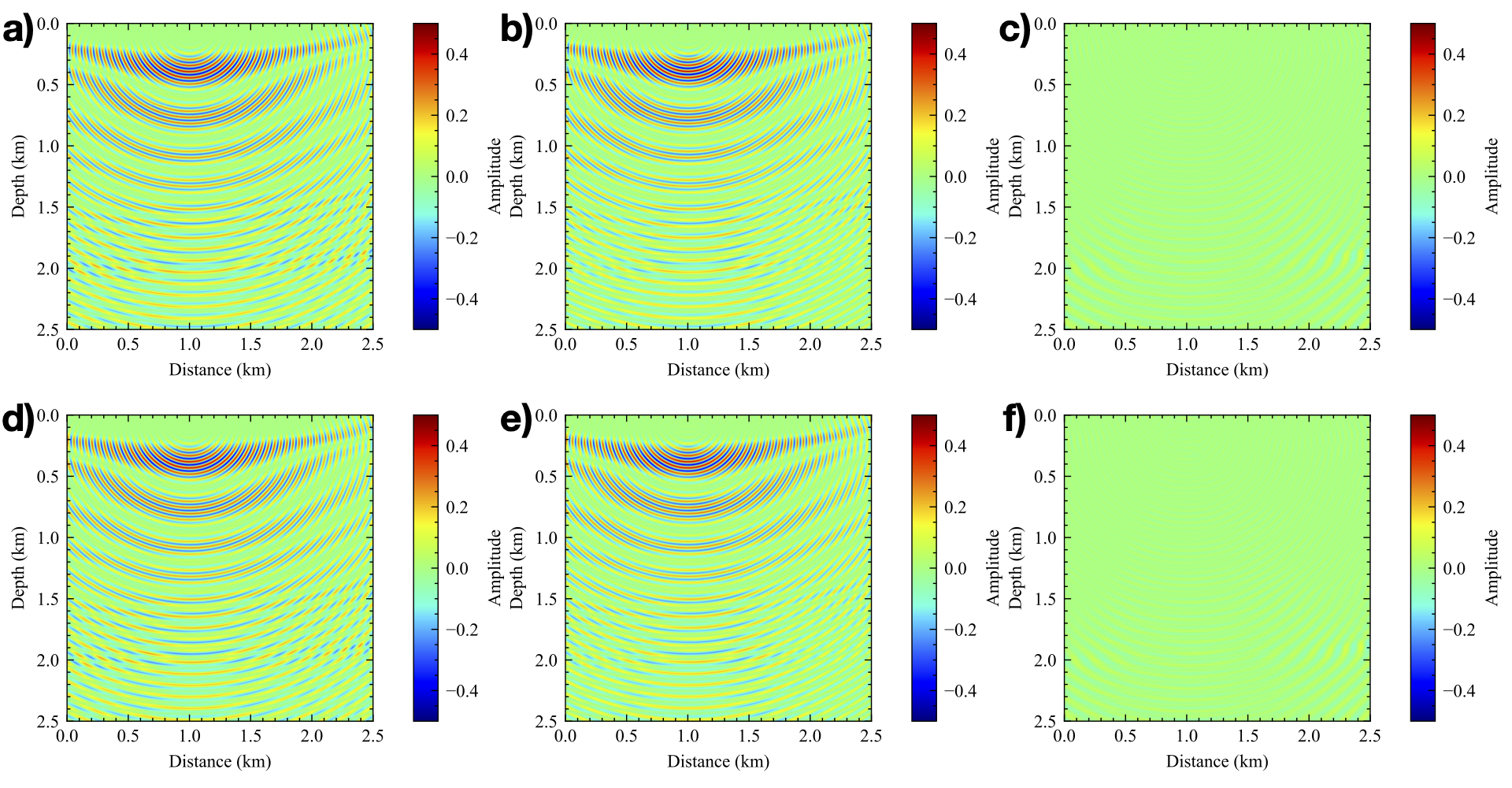
Seismic wave-equation based methods, for example, full waveform inversion, are currently used to illuminate the interior of Earth. Solving for the frequency-domain scattered wavefield via physics-informed neural network (PINN) has great potential in increasing the flexibility and reducing the computational cost of seismic modeling and inversion. However, when dealing with high-frequency wavefields using PINN, its accuracy and training cost limit its application. Thus, we propose a novel implementation of PINN using frequency upscaling and neuron splitting, which allows the neural network model to grow in size as we increase the frequency while leveraging the information from the pre-trained model for lower-frequency wavefields, resulting in fast convergence to highly accurate wavefield solutions. Numerical results show that, compared to the commonly used PINN with random initialization, the proposed PINN exhibits notable superiority in terms of convergence and accuracy and can achieve neuron based high-frequency wavefield solutions with a shallow model.

Theory

Similar to FWI, our NN is first trained for low-frequency wavefields, and gradually optimized for high-frequency wavefields using the lower frequency NN parameters to initialize the model. The information contained in the NN for low-frequency wavefields is beneficial for higher-frequency wavefield training, leading to faster convergence and better prediction than training from scratch. From the prospective of deep learning, our source domain (low-frequency wavefield) and target domain (a higher-frequency wavefield) are inherently related through the kinematic properties for a given velocity model and source location. However, higher frequency wavefields are dynamically more complex, and thus, will require larger neural network models that can represent the complex features. The workflow of the proposed method is illustrated in Figure 1. After we train the neural network to predict low-frequency wavefields using a small network, we increase the size of the network through neural splitting and then use it to learn higher frequency representation. Thus, we can benefit from the NN training experience at low frequency to help us converge faster at high frequencies.

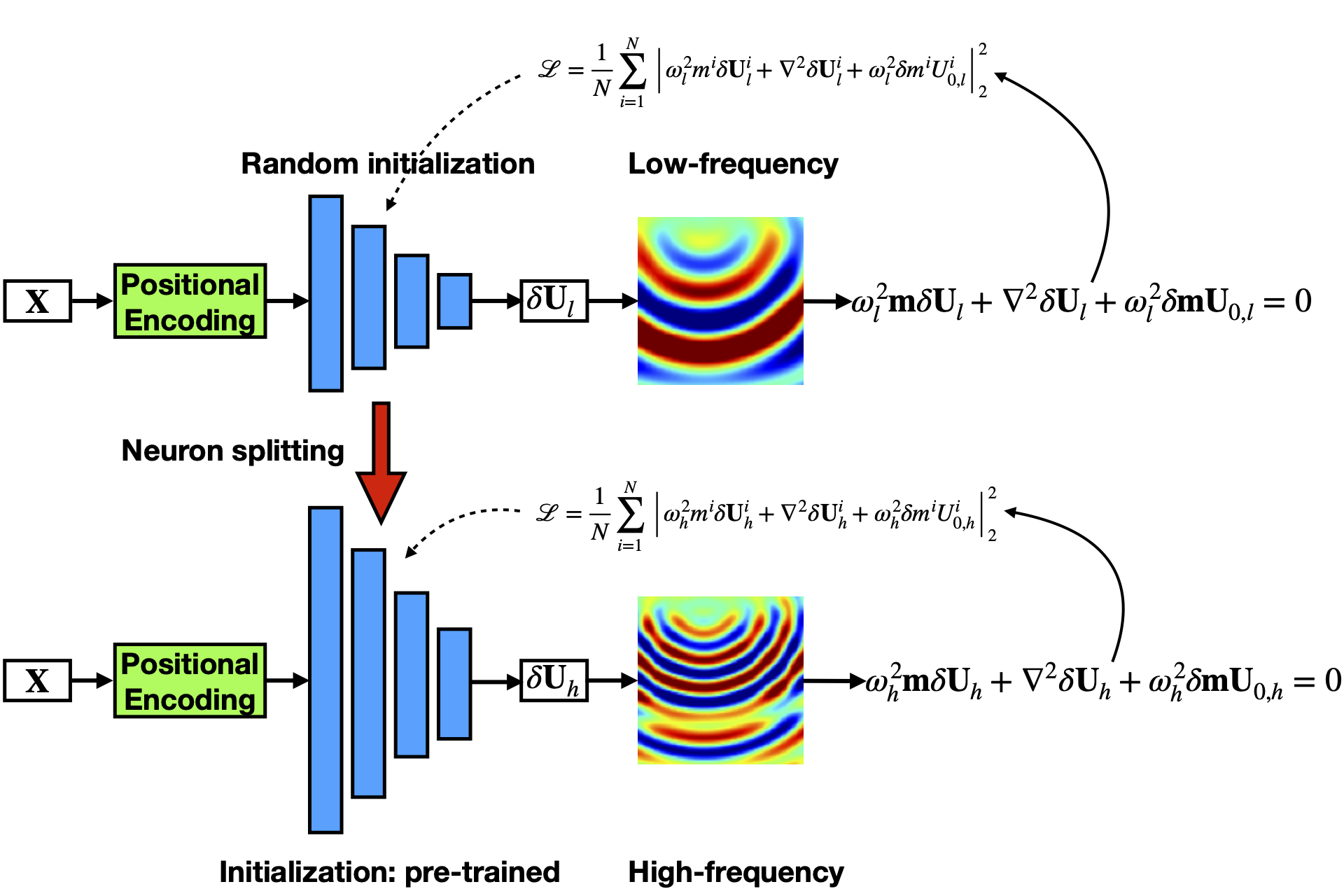
As mentioned before, we want to leverage the information from trained models, while increasing the convergence speed of larger NNs needed for higher frequency representations. The concept of neuron splitting allows us to increase the network size without effecting its output. The splitting process of the neurons in a hidden layer involves duplicating the weights coming into the neuron to all of its off springs, while dividing the weights connecting the neuron with the next layer by the number of offsprings. In the case of splitting all the neurons, the weights and biases are given by the following formulas: \begin{equation} \label{equ:inputl} \mathbf{W}^{(1)}_{split} = \begin{bmatrix} \mathbf{W}^{(1)} \dots \mathbf{W}^{(1)} \end{bmatrix}^T, \mathbf{b}^{(1)}_{split} = \begin{bmatrix} \mathbf{b}^{(1)}\dots\mathbf{b}^{(1)}\end{bmatrix}^T, \end{equation} \begin{equation} \label{equ:hidl} \mathbf{W}^{(\ell)}_{split} = \frac{1}{n}\begin{bmatrix} \mathbf{W}^{(\ell)} \dots \mathbf{W}^{(\ell)} \\ \vdots \\ \mathbf{W}^{(\ell)} \dots \mathbf{W}^{(\ell)} \end{bmatrix}, \mathbf{b}^{(\ell)}_{split} = \begin{bmatrix} \mathbf{b}^{(\ell)}\dots\mathbf{b}^{(\ell)}\end{bmatrix}^T, \end{equation} \begin{equation} \label{equ:outl} \mathbf{W}^{(L)}_{split} = \frac{1}{n}\begin{bmatrix} \mathbf{W}^{(L)} \dots \mathbf{W}^{(L)} \end{bmatrix}, \mathbf{b}^{(L)}_{split} = \mathbf{b}^{(L)}. \end{equation} where the size of the vector and the number of columns in the matrix are equal to $n$.

Results

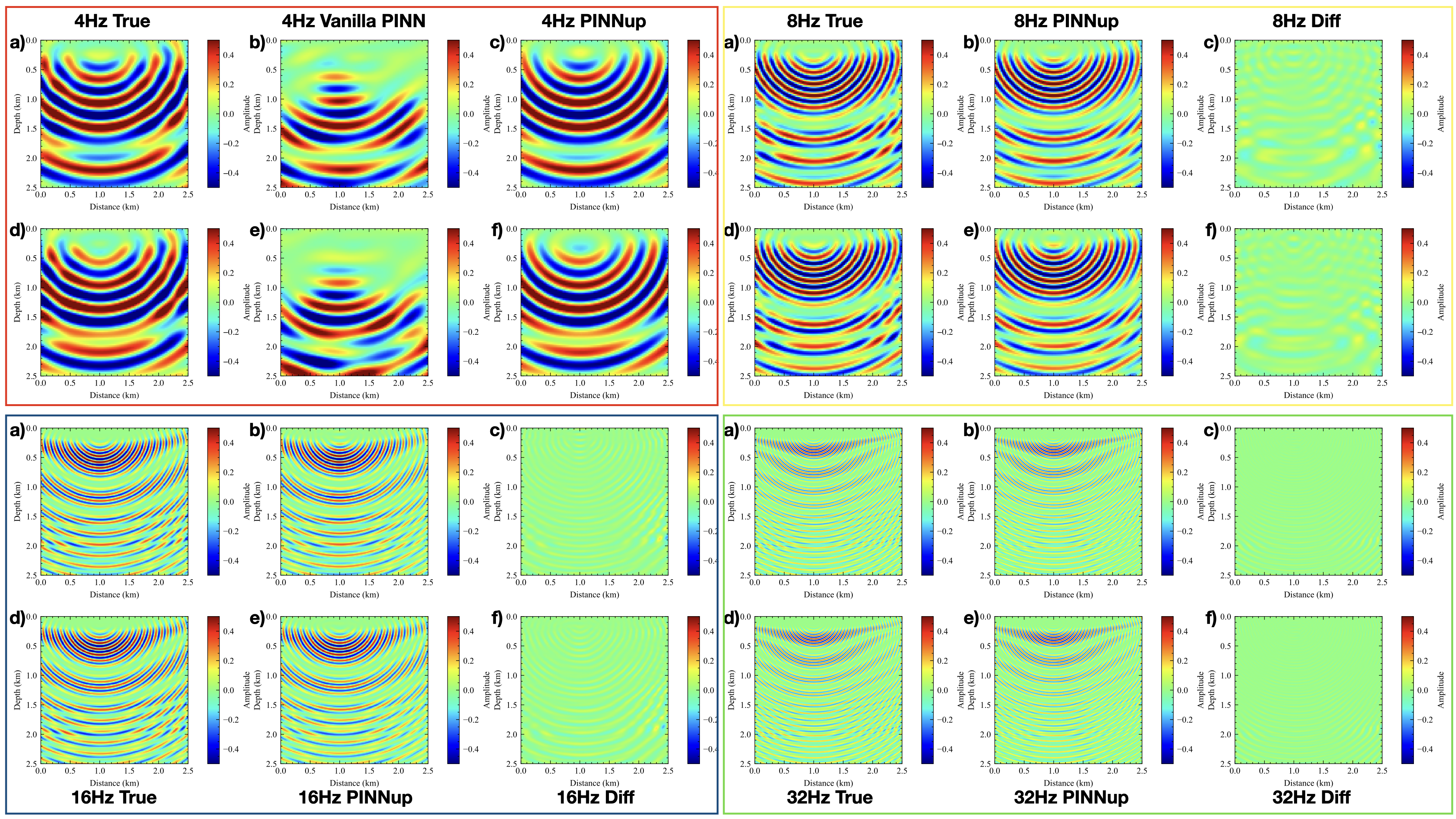
Even though the representations of wavefield via NN at every frequency may include some errors, those errors, as we saw, are generally small, and we managed to capture the most important features of the wavefield. To further highlight the importance of our approach for PINN, we refer the reader to Sitzmann et al. (2020) in which they use a sine activation function to predict a 3.2 Hz wavefield corresponding to the Helmholtz equation, and to do so they needed a network of 5 layers with 256 neurons per layer, and that prediction was for a single source, not a Green's function.

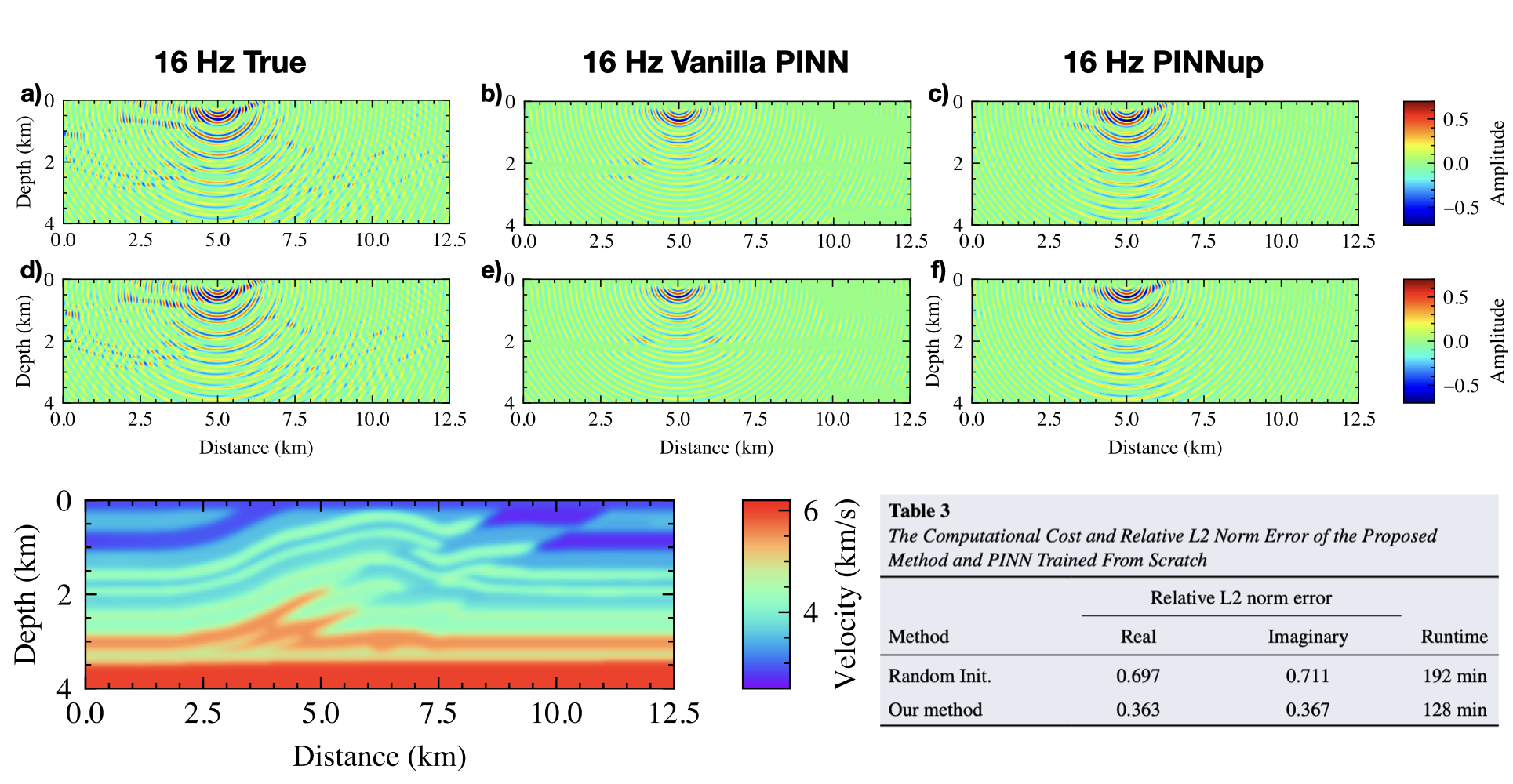
From the experiments, we observe that with our proposed method, we can easily predict highly accurate multi-frequency wavefield solutions at any location in the domain of interest corresponding to any source location on the surface (because the input of our network includes the coordinates of source on the surface and arbitrary space coordinates). In other words, no interpolation is needed. Such a continuous wavefield representation is stored in a much more compressed form even for the 32 Hz representation.

Experiments on the Overthrust model demonstrate that the proposed method outperforms the vanilla PINN in accuracy and efficiency.

Citation

If you found the paper useful, please cite it via:

                  
Huang, X., & Alkhalifah, T. (2022). PINNup: Robust neural network wavefield solutions using frequency upscaling and neuron splitting. Journal of Geophysical Research: Solid Earth, 127, e2021JB023703. https://doi.org/10.1029/2021JB023703

                  
@article{Huang2022PINNup, 
  doi = {10.1029/2021jb023703}, 
  url = {https://doi.org/10.1029%2F2021jb023703}, 
  year = 2022, 
  month = {jun}, 
  volume={127},
  issue={6},
  publisher = {American Geophysical Union ({AGU})}, 
  author = {Xinquan Huang and Tariq Alkhalifah}, 
  title = {{PINNup}: Robust neural network wavefield solutions using frequency upscaling and neuron splitting}, 
  journal = {Journal of Geophysical Research: Solid Earth} }